TimTaiLieu.vn - Tài liệu, ebook, giáo trình, đồ án, luận văn
TimTaiLieu.vn - Thư viện tài liệu, ebook, đồ án, luận văn, tiểu luận, giáo trình các lĩnh vực CNTT, Ngoại ngữ, Luật, Kinh doanh, Tài chính, Khoa học...

 Thuật toán đơn hình mở rộng (bài toán m)
Thuật toán đơn hình mở rộng (bài toán m)2) Quan hệ giữa bài toán xuất phát và bài toán mở rộng: Giả sử (x*, xig) là phương án của bài toán mở rộng, ta có: Nếu x là PA của bài toán xuất phát thì (x*, xig) = (x, 0) là phương án của bài toán mở rộng. Ngược lại phương án của bài toán mở rộng là (x*, xig) = (x, 0) thì x...
 9 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 4774 | Lượt tải: 1
9 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 4774 | Lượt tải: 1 Các tính chất chung của bài toán quy hoạch tuyến tính và phương pháp đơn hình
Các tính chất chung của bài toán quy hoạch tuyến tính và phương pháp đơn hìnhGiải hệ phương trình tuyến tính tổng quát Các bước giải: 1. Lập bảng các hệ số cho hệ đã cho 2. Xác nhận các ẩn cơ sở đã có 3. Tìm thêm ẩn cơ sở mới Chọn ẩn cơ sở xj (xj chưa là ẩn cơ sở) Chọn phần tử chủ yếu aịj trên cột j (điều kiện aij khác 0) Tính các hệ số cho bảng mới theo quy tắc hình chữ nhật.
 22 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 3921 | Lượt tải: 4
22 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 3921 | Lượt tải: 4 Đạo hàm và vi phân
Đạo hàm và vi phânMột số quy tắc đạo hàm - Đạo hàm của tổng hiệu tích thương của 2 hàm số - Đạo hàm của hàm số hợp - Đạo hàm của hàm số ngược - Đạo hàm của hàm số có dạng: y = u(x)v(x) Lưu ý: Trong các qui tắc trên thì qui tắc đạo hàm cảu hàm số hợp là cần được chú ý nhất. Trong nhiều bài tập ta phải áp dụng nhiều lần qui tắc này. Ta còn phải ghi nhớ bảng đạ...
 14 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2584 | Lượt tải: 4
14 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2584 | Lượt tải: 4 Mô hình tối ưu tuyến tính - Quy hoạch tuyến tính
Mô hình tối ưu tuyến tính - Quy hoạch tuyến tínhMột số khái niệm: Vectơ x=( x1, x2,…, xn) được gọi là phương án (PA) của bài toán QHTT nếu nó thỏa mãn hệ ràng buộc của bài toán Phương án x*=( x1*, x2*, …, xn*) được gọi là phương án tối ưu (PATƯ) của bài toán QHTT nếu giá trị hàm mục tiêu tại đó là tốt nhất. Giải bài toán QHTT tức là tìm ph...
 26 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 3120 | Lượt tải: 2
26 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 3120 | Lượt tải: 2 Hệ thức lượng trong tam giác
Hệ thức lượng trong tam giácCho tam giác ABC có BC = a, CA = b, AB = c nội tiếp đường tròn (O; R) Nếu tam giác ABC vuông tại A thì ta có BC = a = 2RsinA CA = b = 2RsinB AB = c = 2RsinC
 17 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2449 | Lượt tải: 1
17 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2449 | Lượt tải: 1 Câu hỏi bài tập toán lớp 10
Câu hỏi bài tập toán lớp 10Câu 2: Định nghĩa hai vectơ cùng phương, cùng hướng, bằng nhau? Trả lời: Hai vectơ cùng phương nếu chúng có giá song song hoặc trùng nhau. Hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng. Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài.
 14 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2333 | Lượt tải: 0
14 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2333 | Lượt tải: 0 Bài 4 Phương trình tích
Bài 4 Phương trình tíchHãy nhớ lại một tính chất của phép nhân các số, phát biểu tiếp các khẳng định sau: Trong một tích, nếu có một thừa số bằng 0 thì tích bằng 0; ngược lại, nếu tích bằng 0 thì ít nhất một trong các thừa số của tích bằng 0 TQ: a.b = 0 <=> a = 0 hoặc b = 0 (a và b là hai số)
 9 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 3746 | Lượt tải: 0
9 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 3746 | Lượt tải: 0 Bài giảng phần lượng giác
Bài giảng phần lượng giác1. Đường tròn lượng giác: A: điểm gốc của cung lượng giác. x'Ox : trục côsin ( trục hoành ) y'Oy : trục sin ( trục tung ) t'At : trục tang u'Bu : trục cotang 2. Định nghĩa các giá trị lượng giác Trong mặt phẳng Oxy cho đường tròn (O;R=1), điểm M(x;y) thuộc (O;R), gọi: ta có:
 220 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 5039 | Lượt tải: 1
220 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 5039 | Lượt tải: 1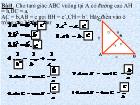 Các hệ thức lượng trong tam giác và giải tam giác
Các hệ thức lượng trong tam giác và giải tam giáca.Bài toán: Hai tàu thuỷ cùng xuất phát từ một vị trí với vận tốc v1=30km/h,v2=50km/h theo hai hướng hợp với nhau một góc (như hình vẽ). Hỏi sau một giờ hai tàu cách nhau bao xa? Từ bài toán trên ta thấy trong một tam giác khi biết hai cạnh và góc xen giữa ta sẽ tính được cạnh còn lại đó chính là định lý cosin Định Lý Cosin Trong tam giác ABC bấ...
 15 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2785 | Lượt tải: 2
15 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2785 | Lượt tải: 2 Chuyên đề Bồi dưỡng năng lực giải toán về đẳng thức và bất đẳng thức cho học sinh giỏi lớp 9 THCS
Chuyên đề Bồi dưỡng năng lực giải toán về đẳng thức và bất đẳng thức cho học sinh giỏi lớp 9 THCSTrong BT này một suy nghĩ tự nhiên có thể nảy sinh là: HĐT nào cho ta mối quan hệ giữa a+ b+ c và a2+b2+c2; giữa a2+b2+c2 và a4 + b4 + c4. Hoặc là: Từ giả thiết có mối quan hệ b + c = -a. Vậy HĐT nào cho ta mối quan hệ giữa b2, c2 và a2; giữa b4, c4 và a4 ? Bình phương 2 vế của ĐT -a = (b + c) ta được: a2 = b2 + 2bc + c2 <=> 2bc = a2 - b2 - c2
 107 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 13198 | Lượt tải: 1
107 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 13198 | Lượt tải: 1
Website đang trong thời gian thử nghiệm, chờ xin giấy phép của Bộ TT & TT.

