TimTaiLieu.vn - Tài liệu, ebook, giáo trình, đồ án, luận văn
TimTaiLieu.vn - Thư viện tài liệu, ebook, đồ án, luận văn, tiểu luận, giáo trình các lĩnh vực CNTT, Ngoại ngữ, Luật, Kinh doanh, Tài chính, Khoa học...

 Tính nửa liên tục trên của ánh xạ nghiệm cho bài toán bất đẳng thức tựa biến phân vectơ hỗn hợp phụ thuộc tham số loại Minty
Tính nửa liên tục trên của ánh xạ nghiệm cho bài toán bất đẳng thức tựa biến phân vectơ hỗn hợp phụ thuộc tham số loại MintyTÓM TẮT Trong bài báo này, đầu tiên chúng tôi nghiên cứu một lớp bài toán bất đẳng thức tựa biến phân vectơ hỗn hợp phụ thuộc tham số loạiMinty trong không gian vectơ tôpô Hausdorff lồi địa phương, bài toán này chứa rất nhiều bài toán như là các trường hợp đặc biệt, cụ thể là: bài toán điểm bất động, bài toán điểm trùng, bài toán bù, bài toán t...
 5 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 538 | Lượt tải: 0
5 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 538 | Lượt tải: 0 Đề cương chi tiết học phần Thực tập nghề nghiệp 2 - Phân tích chính sách nông thôn
Đề cương chi tiết học phần Thực tập nghề nghiệp 2 - Phân tích chính sách nông thôn1. Tên học phần: Thực tập nghề nghiệp 2 Phân tích chính sách nông thôn - Mã số học phần: RDE 412 - Số tín chỉ: 01 - Trình độ: Cho sinh viên năm thứ 3 - Tính chất của học phần: Bắt buộc - Học phần thay thế, tương đương: Không - Ngành (chuyên ngành) đào tạo: Phát triển nông thôn 2. Phân bổ thời gian học tập - Số tiết thực tập tại trường : 0...
 4 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 966 | Lượt tải: 0
4 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 966 | Lượt tải: 0 Đề thi cuối kỳ học kỳ I môn Phương pháp tính - Đề thi số 101010 - Năm học 2018-2019 - Đại học Sư phạm Kỹ thuật TP.HCM
Đề thi cuối kỳ học kỳ I môn Phương pháp tính - Đề thi số 101010 - Năm học 2018-2019 - Đại học Sư phạm Kỹ thuật TP.HCMa. Áp dụng công thức trên tính gần đúng 1 = [ Vefdx = (16), khi đó sai số tuyệt đối là (17). Nếu tính I bằng công thức Simpson 4 đoạn chia thì sai số tuyệt đối không quá (18). b. Trong ý (19), hãy nêu một sự khác biệt giữa công thức Simpsom 3:8 và công thức Simpson. Trong ý (20), hãy nêu một ưu điểm về sai số của công thức Simpsom 3:8 so với côn...
 4 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 564 | Lượt tải: 0
4 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 564 | Lượt tải: 0 Đề thi cuối học kỳ môn Đại số B1 (Khóa 2013) - Đại học Khoa học Tự nhiên TP.HCM
Đề thi cuối học kỳ môn Đại số B1 (Khóa 2013) - Đại học Khoa học Tự nhiên TP.HCMBài 3: (2,0 điểm). a) Cho V là một không gian vectơ trên ℝ và u, v ϵ V. Chứng minh rằng {u; v} độc lập tuyến tính khi và chỉ khi {u + v; u − v} độc lập tuyến tính. b) Cho W = {(x; y; z) ϵ ℝ3|x + 2y = 3z}, W′ = {(x; y; z) ϵ ℝ3 |xy = z2}. Kiểm tra W và W′có là không gian con của không gian vectơ ℝ3 hay không? Giải thích?
 3 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 599 | Lượt tải: 0
3 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 599 | Lượt tải: 0 Đề thi cuối học kỳ môn Đại số B1 (Khóa 2012) - Đại học Khoa học Tự nhiên TP.HCM
Đề thi cuối học kỳ môn Đại số B1 (Khóa 2012) - Đại học Khoa học Tự nhiên TP.HCMBài 2: Cho W là không gian con của R3 sinh bởi các vecto u1 = (1; 1; 2); u2 = (1; 2; 1); u3 = (1; -1; 4). a) Tìm một cơ sở và xác định chiều của không gian W. b) Xác định m để vecto u = (m; 4; m + 2) thuộc W. Bài 3: Trong không gian R3 cho các vecto u1 = (1; 2; 3); u2 = (1; 3; 2); u3 = (2; 5; 4) và u = (3; 8; 4). a) Chứng minh tập hợp B = {u1...
 3 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 771 | Lượt tải: 0
3 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 771 | Lượt tải: 0 Đề thi cuối học kỳ môn Đại số B1 (Khóa 2011) - Đại học Khoa học Tự nhiên TP.HCM
Đề thi cuối học kỳ môn Đại số B1 (Khóa 2011) - Đại học Khoa học Tự nhiên TP.HCMBài 3: Cho B = {u1, u2, u3} và B' = {u1', u2', u3'} là hai cơ sở của R3 sao cho u1 = (1;-1;1), u2 = (1;2;3), u3 = (2;-1;3) và ma trận chuyển cơ sở từ B sang B' là a) Hãy xác định cơ sở B'. b) Hãy xác định ma trận chuyển cơ sở từ B' sang B.
 1 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 513 | Lượt tải: 0
1 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 513 | Lượt tải: 0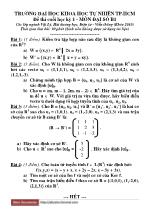 Đề thi cuối học kỳ môn Đại số B1 (Khóa 2010) - Đại học Khoa học Tự nhiên TP.HCM
Đề thi cuối học kỳ môn Đại số B1 (Khóa 2010) - Đại học Khoa học Tự nhiên TP.HCMBài 2: (3 điểm). Cho W là không gian con của không gian R* sinh bởi các vectơ u = (1,1,1,1), u = (1,2,3,3), u3 = (1,3,4,2), u4 = (1,2,1,-3). a) Chứng minh tập hợp B = {uh, uh, us} là cơ sở của W và xác định [u]B. b) Cho u = (m, m – 1, 2m, m - 2) + R'. Hãy tìm giá trị của | m để u 6 W. Với giá trị m vừa tìm được, hãy biểu diễn vectơ u dưới dạng t...
 3 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 473 | Lượt tải: 0
3 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 473 | Lượt tải: 0 Đề thi cuối học kỳ môn Đại số B1 (Khóa 2009) - Đại học Khoa học Tự nhiên TP.HCM
Đề thi cuối học kỳ môn Đại số B1 (Khóa 2009) - Đại học Khoa học Tự nhiên TP.HCMBài 1: (2,0 điểm). a) Cho ( ) Chứng minh rằng A khả nghịch khi và chỉ khi adj(A) khả nghịch (trong đó adj(A) là ma trận phó của A). b) Cho ( ) Chứng minh rằng AB khả nghịch khi và chỉ khi cà A và B cùng khả nghịch. Bài 2: (2,0 điểm). Trong R4 cho các vectơ ( ), ( ), ( ) và W là không gian con của R4 sinh bởi các vectơ . a) Chứng minh rằng tập hợp *...
 2 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 567 | Lượt tải: 0
2 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 567 | Lượt tải: 0 Bài giảng Phương pháp tham lam (Bản đẹp)
Bài giảng Phương pháp tham lam (Bản đẹp)+ Cho trước một tập A gồm n đối tượng, ta cần phải chọn một tập con S từ tập A. Với mỗi tập con S được chọn ra thỏa mãn các yêu cầu của bài toán, ta gọi là một nghiệm chấp nhận được. Nghiệm tối ưu là nghiệm chấp nhận được mà tại đó hàm mục tiêu đạt giá trị nhỏ nhất (lớn nhất). Ý tưởng tham lam: Xây dựng lời giải của bài toán với việc chấp nhận ...
 24 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 523 | Lượt tải: 0
24 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 523 | Lượt tải: 0 Phân tích dao động tự do vỏ trụ tròn bằng vật liệu rỗng theo lý thuyết biến dạng cắt bậc nhất
Phân tích dao động tự do vỏ trụ tròn bằng vật liệu rỗng theo lý thuyết biến dạng cắt bậc nhấtTÓM TẮT Bài báo sử dụng lý thuyết biến dạng cắt bậc nhất (FSDT) của Reissner-Mindlin để xây dựng lời giải tích phân tích dao động tự do của vỏ trụ tròn làm bằng vật liệu rỗng, tựa khớp trên hai cạnh biên. Mô đun đàn hồi và khối lượng riêng của vật liệu được giả thiết là hàm số của lỗ rỗng, biến đổi trơn và đối xứng theo phương chiều dày vỏ. Hệ ...
 10 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 612 | Lượt tải: 0
10 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 612 | Lượt tải: 0
Website đang trong thời gian thử nghiệm, chờ xin giấy phép của Bộ TT & TT.

