TimTaiLieu.vn - Tài liệu, ebook, giáo trình, đồ án, luận văn
Tổng hợp tất cả tài liệu, ebook, giáo trình Công Nghệ Thông Tin chọn lọc và hay nhất.

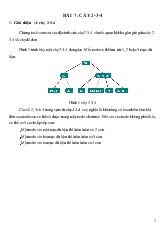 Bài giảng Cây 2-3-4
Bài giảng Cây 2-3-4Chúng ta sẽ xem xét các đặc tính của cây 2-3-4 và mối quan hệ khá gần gũi giữa cây 2-3-4 và cây đỏ-đen. Hình 1 trình bày một cây 2-3-4 đơn giản. Mỗi node có thể lưu trữ 1, 2 hoặc 3 mục dữ liệu. Các số 2, 3 và 4 trong cụm từ cây 2-3-4 có ý nghĩa là khả năng có bao nhiêu liên kết đến các node con có thể có được trong một node cho trước. Đối với cá...
 12 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2222 | Lượt tải: 1
12 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2222 | Lượt tải: 1 Bài giảng bài 13: Cây đỏ đen
Bài giảng bài 13: Cây đỏ đenTuy nhiên trong một số trường hợp cây tìm kiếm nhị phân có một số hạn chế. Nó hoạt động tốt nếu dữ liệu được chèn vào cây theo thứ tự ngẫu nhiên. Tuy nhiên, nếu dữ liệu được chèn vào theo thứ tự đã đuợc sắp xếp sẽ không hiệu quả. Khi các trị số cần chèn đã đuợc sắp xếp thì cây nhị phân trở nên không cân bằng. Khi cây không cân bằng, nó mất đi khả n...
 13 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2343 | Lượt tải: 1
13 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2343 | Lượt tải: 1 Bài giảng Cây cân bằng
Bài giảng Cây cân bằngMột cây rất khó đạt được trạng thái cân bằng hoàn toàn và cũng rất dễ mất cân bằng vì khi thêm hay hủy các nút trên cây có thể làm cây mất cân bằng, chi phí cân bằng lại cây cao vì phải thao tác trên toàn bộ cây. Đối với cây cân bằng hoàn toàn, trong trường hợp xấu nhất ta chỉ phải tìm qua log2N phần tử (N là số nút trên cây). Sau đây là ví dụ ...
 11 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2160 | Lượt tải: 1
11 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2160 | Lượt tải: 1 Bài giảng Cây, cây nhị phân, cây nhị phân tìm kiếm
Bài giảng Cây, cây nhị phân, cây nhị phân tìm kiếmCây là một tập hợp T các phần tử (nút trên cây) trong đó có 1 nút đặc biệt T0 được gọi là gốc, các nút còn khác được chia thành những tập rời nhau T1, T2 , . , Tn theo quan hệ phân cấp trong đó Ti cũng là một cây. Nút ở cấp i sẽ quản lý một số nút ở cấp i+1. Quan hệ này người ta còn gọi là quan hệ cha-con.
 11 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2979 | Lượt tải: 2
11 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2979 | Lượt tải: 2 Bài giảng bài 5: Bảng băm (hash table)
Bài giảng bài 5: Bảng băm (hash table)Phép băm được đề xuất và hiện thực trên máy tính từ những năm 50 của thế kỷ 20. Nó dựa trên ý tưởng: biến đổi giá trị khóa thành một số (xử lý băm) và sử dụng số này để đánh chỉ cho bảng dữ liệu. Các phép toán trên các cấu trúc dữ liệu như danh sách, cây nhị phân, phần lớn được thực hiện bằng cách so sánh các phần tử của cấu trúc, do vậy thời gia...
 16 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2458 | Lượt tải: 2
16 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2458 | Lượt tải: 2 Bài giảng Một số phương pháp sắp xếp
Bài giảng Một số phương pháp sắp xếpÝ tưởng: Có dãy số: a1, a2, ., an Giải thuật QuickSort làm việc như sau: Chọn x là một phần tử làm biên: thường chọn là phần tử ở giữa dãy số. Phân hoạc dãy thành 3 dãy con 1. ak <= x , với k = 1.i 2. ak = x , với k = i.j 3. ak > =x , với k = j.N
 15 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2327 | Lượt tải: 2
15 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2327 | Lượt tải: 2 Bài giảng Cấu trúc dữ liệu và thuật toán: List, stack và queue
Bài giảng Cấu trúc dữ liệu và thuật toán: List, stack và queueCác khai báo cần thiết là typedef . ElementType; //kiểu phần tử trong danh sách typedef struct Node { ElementType Element;//Chứa nội dung của phần tử Node* Next; /*con trỏ chỉđến phần tử kế tiếp trong danh sách*/ }; typedef Node* Position; // Kiểu vị trí typedef Position List;
 29 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2899 | Lượt tải: 1
29 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2899 | Lượt tải: 1 Bài giảng Cấu trúc dữ liệu và thuật toán: Tìm kiếm cây đỏ đen và các cây cân bằng động khác
Bài giảng Cấu trúc dữ liệu và thuật toán: Tìm kiếm cây đỏ đen và các cây cân bằng động khácCây Đỏ -Đen (Red-Black) • Một thuật toán phức tạp • Cho O(log n) với Thêm(addition), Xóa(deletion) và Tìm(search) • Các kỹ thuật phần mềm • Biết về thuật toán • Biết khi nào có thể dùng chúng • Biết về hiệu suất • Biết nơi có thể áp dụng • Đủthông minh để dùng cho các máy phát minh. • Họ sử dụng lại bộ mã • Vì thế họ cần nhiều thời gian h...
 28 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 3393 | Lượt tải: 2
28 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 3393 | Lượt tải: 2 Bài giảng Cấu trúc dữ liệu và thuật toán: Tìm kiếm
Bài giảng Cấu trúc dữ liệu và thuật toán: Tìm kiếmCây nhị phân O(log n) nếu nó là cây cân bằng • Cây nhịphân đơn giản tốt cho các mảng tĩnh • Tần xuất thấp (preferably zero) cho insertions/deletions Nhưng bộ dữ liệu của tôi có thể thay đổi! • Bộ dữ liệu động • Cần thiết phải tạo ra cây cân bằng • Đầu tiên, kiểm tra một vài hoạt động của cây cơ bản. • Hữu ích trong một vài cách!
 37 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 1980 | Lượt tải: 1
37 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 1980 | Lượt tải: 1 Bài giảng Cấu trúc dữ liệu và thuật giải: Tìm kiếm
Bài giảng Cấu trúc dữ liệu và thuật giải: Tìm kiếm• Tìm kiếm tuần tự • Thời gian tồi nhất là n • Chúng tôi có Độ phức tạp O(n) • Ứng dụng cho mảng (không sắp xếp) và danh sách liên kết • Tìm kiếm nhị phân • Ứng dụng cho dãy đã sắp xếp • Thời gian thực hiện thuật toán log2n • Độ phức tạp tính toán O(log n)
 16 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2104 | Lượt tải: 1
16 trang | Chia sẻ: haohao89 | Ngày: 29/07/2013 | Lượt xem: 2104 | Lượt tải: 1
Website đang trong thời gian thử nghiệm, chờ xin giấy phép của Bộ TT & TT.

