TimTaiLieu.vn - Tài liệu, ebook, giáo trình, đồ án, luận văn
Tổng hợp tất cả tài liệu, ebook, giáo trình Toán - Thống Kê chọn lọc và hay nhất.

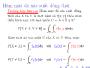 Hàm mật độ xác suất đồng thời
Hàm mật độ xác suất đồng thờiTrường hợp liên tục Hàm mật độ xác suất đồng thời của X và Y là một hàm số f(x,y) thỏa mãn điều kiện sau: Với mọi miến C = AxB thuộc R2 Hàm mật độ xác suất lề của X và Y thỏa mãn:
 10 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 5365 | Lượt tải: 0
10 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 5365 | Lượt tải: 0 Hàm mật độ xác suất (Probability Density Function - Pdf)
Hàm mật độ xác suất (Probability Density Function - Pdf)Biến rời rạc Hàm mật độ xác suất của biên ngẫu nhiên rời rác X, ký hiệu là f(x), được định nghĩa bởi: f(x) = P(X = x) trong đó x là các giá trị của biến ngẫu nhiên X.
 10 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 2824 | Lượt tải: 0
10 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 2824 | Lượt tải: 0 Biến ngẫu nhiên và kỳ vọng
Biến ngẫu nhiên và kỳ vọngMột biến ngẫu nhiên (random variable), ký hiệu X, là một hàm số xác định trên không gian mẫu S, cho tương ứng mỗi phần tử e của tập S với 1 số thực x. X: S -> R e -> X(e) = x Xét một con xúc sắc 4 mặt có in các số 1,2,3,4. Tung xúc sắc 2 lần, điểm có được của người chơi là số lớn nhất hiện ra sau 2 lần tung. Khi đó ta có thể xem số điểm có được...
 10 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 2567 | Lượt tải: 0
10 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 2567 | Lượt tải: 0 Đại số Boolean và cổng luận lý
Đại số Boolean và cổng luận lýCơ sở toán họccho các hệ thống số là đại số Boolean (Boolean algebra) George Boole giới thiệu vào năm 1854 Tương tự các hệ đại số khác, được xây dựng thông qua việc xác định nghĩa những vấn đề cơ bản sau: Miền(domain), là tập hợp (set) các phần tử(element) mà trên đó định nghĩa nên hệ đại số Các phép toán(operation) thực hiện được trên mi...
 74 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 3513 | Lượt tải: 1
74 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 3513 | Lượt tải: 1 Chuỗi hàm phức
Chuỗi hàm phứcĐịnh lí 1: Nếu tất cả các số hạng un(z) của chuỗi hàm (10) đều liên tục trong miền G và nếu chuỗi hàm (1) hội tụ đều trong G thì tổng f(z) của nó cũng liên tục trong G. Chứng minh: Giả sử z và z + h là hai điểm bất kì trong G. Ta có: f(z) = Sn(z) + Rn(z) f(z + h) = Sn(z + h) + Rn(z + h)
 19 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 4344 | Lượt tải: 1
19 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 4344 | Lượt tải: 1 Hàm số nhiều biến số
Hàm số nhiều biến sốNếu người ta cho hàm số hai biến số bởi biểu thức z = f(x, y) mà không nói gì về miền xác định của nó thì miền xác định của hàm số đó được hiểu là tập hợp những cặp (x, y) sao cho biểu thức f(x, y) có nghĩa. Ví dụ1: Hàm số z = 2x - 3y + 5 xác định với mọi cặp (x, y) thuộc R2 , miền xác định của nó là toàn bộ mặt phẳng
 24 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 3212 | Lượt tải: 0
24 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 3212 | Lượt tải: 0 Phép tính vi phân hàm một biến
Phép tính vi phân hàm một biếnVí dụ2.Trong ví dụ1 Dãy a) là dãy số giảm, nó bị chặn dưới bởi 0 và bị chặn trên bởi 1; Dãy b) không phải là dãy số đơn điệu, nó bịchặn dưới bởi -1 và bị chặn trên bởi 1; Dãy c) là dãy tăng, nó bị chặn dưới bởi 1 nhưng không bị chặn trên, do đó nó không bị chặn; Dãy d) là dãy số tăng, nó bịchặn dưới bởi 0 và bị chặn trên bởi 1.
 62 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 2348 | Lượt tải: 0
62 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 2348 | Lượt tải: 0 Phương trình lượng giác phương trình – bất phương trình – hệ phương trình đại số
Phương trình lượng giác phương trình – bất phương trình – hệ phương trình đại sốb) Công thức nhân 1) sin2a = 2sinacosa 2)cos2a = cos2a - sin2a = 1 - 2sin2a = 2cos2a - 1 3) sin3a = 3sina - 4sin3a 4) cos3a = 4cos3a - 3cosa
 46 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 2709 | Lượt tải: 1
46 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 2709 | Lượt tải: 1 Các chú ý và lời giải cho một số bài toán cơ bản
Các chú ý và lời giải cho một số bài toán cơ bản- Khi rút gọn các biểu thức là các phép tính giữa các phân thức ta thường tìm cách đưa biểu thức thành một phân thức sau đó phân tích tử và mẫu thành nhân tử rồi giản ước những thừa số chung của cả tử và mẫu. - Trường hợp đề bài không cho điều kiện thì khi rút gọn xong ta nên tìm điều kiện cho biểu thức. Khi đó quan sát biểu thức cuối cùng và các ...
 13 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 2340 | Lượt tải: 0
13 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 2340 | Lượt tải: 0 Các bài toán về lượng giác trong các đề thi Đại học- Cao đẳng 2002-2009
Các bài toán về lượng giác trong các đề thi Đại học- Cao đẳng 2002-2009B-2006 cot x + sin x(1 + tan x tan x/2) = 4 D-2006 cos3x + cos2x - cosx - 1 = 0 A-2005 cos2 3xcos2x - cos2 x = 0 B-2005 1 + sinx + cosx + sin2x + cos2x = 0
 7 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 2811 | Lượt tải: 2
7 trang | Chia sẻ: lylyngoc | Ngày: 21/03/2014 | Lượt xem: 2811 | Lượt tải: 2
Website đang trong thời gian thử nghiệm, chờ xin giấy phép của Bộ TT & TT.

