TimTaiLieu.vn - Tài liệu, ebook, giáo trình, đồ án, luận văn
Tổng hợp tất cả tài liệu, ebook, giáo trình Toán - Thống Kê chọn lọc và hay nhất.

 Bài giảng phần lượng giác
Bài giảng phần lượng giác1. Đường tròn lượng giác: A: điểm gốc của cung lượng giác. x'Ox : trục côsin ( trục hoành ) y'Oy : trục sin ( trục tung ) t'At : trục tang u'Bu : trục cotang 2. Định nghĩa các giá trị lượng giác Trong mặt phẳng Oxy cho đường tròn (O;R=1), điểm M(x;y) thuộc (O;R), gọi: ta có:
 220 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 5041 | Lượt tải: 1
220 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 5041 | Lượt tải: 1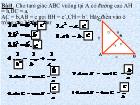 Các hệ thức lượng trong tam giác và giải tam giác
Các hệ thức lượng trong tam giác và giải tam giáca.Bài toán: Hai tàu thuỷ cùng xuất phát từ một vị trí với vận tốc v1=30km/h,v2=50km/h theo hai hướng hợp với nhau một góc (như hình vẽ). Hỏi sau một giờ hai tàu cách nhau bao xa? Từ bài toán trên ta thấy trong một tam giác khi biết hai cạnh và góc xen giữa ta sẽ tính được cạnh còn lại đó chính là định lý cosin Định Lý Cosin Trong tam giác ABC bấ...
 15 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2787 | Lượt tải: 2
15 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2787 | Lượt tải: 2 Chuyên đề Bồi dưỡng năng lực giải toán về đẳng thức và bất đẳng thức cho học sinh giỏi lớp 9 THCS
Chuyên đề Bồi dưỡng năng lực giải toán về đẳng thức và bất đẳng thức cho học sinh giỏi lớp 9 THCSTrong BT này một suy nghĩ tự nhiên có thể nảy sinh là: HĐT nào cho ta mối quan hệ giữa a+ b+ c và a2+b2+c2; giữa a2+b2+c2 và a4 + b4 + c4. Hoặc là: Từ giả thiết có mối quan hệ b + c = -a. Vậy HĐT nào cho ta mối quan hệ giữa b2, c2 và a2; giữa b4, c4 và a4 ? Bình phương 2 vế của ĐT -a = (b + c) ta được: a2 = b2 + 2bc + c2 <=> 2bc = a2 - b2 - c2
 107 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 13202 | Lượt tải: 1
107 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 13202 | Lượt tải: 1 Hình hộp chữ nhật. hình lập phương
Hình hộp chữ nhật. hình lập phươngb) Biết hình hộp chữ nhật có chiều dài 6cm, chiều rộng 3cm, chiều cao 4cm.Tính diện tích của mặt đáy MNPQ và các mặt bên ABNM,BCPN Diện tích mặt bên BCPN là: 3 x 4 = 12 (cm² ) Đáp số: 18cm²; 24cm²;12cm²
 14 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2494 | Lượt tải: 1
14 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2494 | Lượt tải: 1 Hàm số liên tục
Hàm số liên tụcHàm số liên tục trên một khoảng, trên một đoạn Định nghĩa a) Giả sử hàm số f xác định trên tập hợp J, trong đó J là một khoảng hoặc hợp của nhiều khoảng. Ta nói rằng hàm số f liên tục trên J nếu nó liên tục tại mọi điểm thuộc tập hợp đó. b) B) Hàm số f xác định trên đoạn [a;b] được gọi là liên tục trên đoạn [a;b] nếu nó liên tục trên khoảng (a;b...
 9 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2619 | Lượt tải: 2
9 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2619 | Lượt tải: 2 Các trường hợp bằng nhau của tam giác vuông
Các trường hợp bằng nhau của tam giác vuông1) Các trường hợp bằng nhau đã biết của hai tam giác vuông Trên hình vẽ bên em hãy bổ sung thêm các điều kiện về cạnh hay về góc để được các tam giác vuông bằng nhau theo từng trường hợp đã học. TH1 Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau TH2 Nếu một cạnh ...
 17 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 5487 | Lượt tải: 1
17 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 5487 | Lượt tải: 1 Bài 4 Các phép biến đổi
Bài 4 Các phép biến đổiMục đích của các phép biến đổi là đưa các yếu tố hình học ở vị trí tổng quát về vị trí đặc biệt để thuận lợi cho việc giải các bài toán. Dưới đây là một số phương pháp biến đổi. Thay mặt phẳng П1 thành mặt phẳng П’1 Điều kiện: * Xây dựng phép thay mặt phẳng hình chiếu: - Gọi x’ ≡ П’1∩П2 là trục hình chiếu mới. - Giả sử điểm A tron...
 14 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 3434 | Lượt tải: 2
14 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 3434 | Lượt tải: 2 Dãy số có giới hạn vô cực
Dãy số có giới hạn vô cựcĐịnh nghĩa Ta nói rắng dãy số (un) có giới hạn là +∞ nếu với mỗi số dương tùy ý cho trước, mọi số hạng của dãy số, kể từ một số hạng nào đó trở đi, đều lớn hơn số dương đó. Khi đó ta viết Lim(un) = +∞ hoặc limun = +∞ hoặc un -> +∞
 8 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2565 | Lượt tải: 0
8 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2565 | Lượt tải: 0 Dấu của nhị thức bậc nhất
Dấu của nhị thức bậc nhấtNhị thức bậc nhất Nhị thức bậc nhất đối với x là biểu thức có dạng f(x) = ax + b trong đó a, b là hao số đã cho, a ≠ 0 Ví dụ 1: a. Giải bất phương trình -2x + 3 > 0 và biểu diễn trên trục số tập nghiệm của nó. b. Từ đó chỉ ra các khoảng mà nếu x lấy giá trị trong đó thì nhị thức f(x)= -2x + 3 có giá trị c. B.1 Trái dấu với hệ số của x? d. B.b...
 44 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2501 | Lượt tải: 0
44 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2501 | Lượt tải: 0 Bài 3 Mặt phẳng
Bài 3 Mặt phẳngChú ý: Từ cách xác định mặt phẳng này có thể chuyển đổi thành cách xác định khác. Do đó phương pháp giải bài toán không phụ thuộc vào cách cho mặt phẳng Cho mặt phẳng (α): * Vết đứng m: m ≡ (α) ∩ П1 * Vết bằng n: n ≡ (α) ∩ П2 * Vết cạnh p: p ≡ (α) ∩ П3 Để phân biệt các mặt phẳng ta viết tên vết của mặt phẳng kèm theo tên của mặ...
 42 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2583 | Lượt tải: 0
42 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2583 | Lượt tải: 0
Website đang trong thời gian thử nghiệm, chờ xin giấy phép của Bộ TT & TT.

