TimTaiLieu.vn - Tài liệu, ebook, giáo trình, đồ án, luận văn
Tổng hợp tất cả tài liệu, ebook, giáo trình Toán - Thống Kê chọn lọc và hay nhất.

 Đạo hàm – vi phân
Đạo hàm – vi phânHàm số f(x) có đạo hàm trên khoảng (a,b) nếu nó có đạo hàm tại mọi điểm trong khoảng đó, f(x) có đạo hàm trên đoạn [a,b] nếu nó có đạo hàm tại mọi điểm trong khoảng (a,b), có đạo hàm phải tại a và đạo hàm trái tại b
 29 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2717 | Lượt tải: 3
29 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2717 | Lượt tải: 3 Phương trình bậc nhất đối với sinx, cosx
Phương trình bậc nhất đối với sinx, cosx1. Phương pháp giải tổng quát phương trình Asinx + Bcosx + C = 0 2. Các thí dụ 3. Giải phương trình dạng asinu + bcosu = √(a2+b2) cosv 4. Giải phương trình dạng a(sinu + cosv) + b(sinv + cosu) = 0 5. Điều kiện để phương trình có nghiệm 6. Sử dụng công thức cộng chung
 21 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2364 | Lượt tải: 0
21 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2364 | Lượt tải: 0 Căn bậc hai của số phức và phương trình bậc hai
Căn bậc hai của số phức và phương trình bậc haiCho số phức w, mỗi số phức z thỏa mãn z2 = w được gọi là căn bậc hai của số phức w. Giả sử: a + bi = (x + yi)2 <=> a + bi = x2 - y2 + 2xyi
 22 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2811 | Lượt tải: 0
22 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2811 | Lượt tải: 0 Vi tích phân
Vi tích phânĐịnh nghĩa ánh xạ: Cho X, Y là hai tập bất kỳ. Nếu x 𝟄 X, cho tương ứng duy nhất một y = f(x) 𝟄 Y theo qui tắc f, thì f gọi là một ánh xạ từ X vào Y. Ký hiệu: Đơn ánh: với mọi x1, x2 𝟄 X, x1 ≠ x2 => f(x1) ≠ f(x2) Toàn ánh: Với mỗi y 𝟄 Y, tồn tại x 𝟄 X: y = f(x) Song ánh: Nếu f vừa là đơn ánh và toàn ánh Nếu f: X->Y là song ánh thì f-1...
 33 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2713 | Lượt tải: 0
33 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2713 | Lượt tải: 0 Hạng ma trận
Hạng ma trậnCho A là ma trận cấp mxn. Ma trận được tạo ra thành từ các phần tử nằm ở gần giao giữa r và cột của ma trận A gọi là ma trận con cấp r của A. Định thức của ma trận con cấp r cảu A coi là định thức con cấp r cảu A.
 20 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2758 | Lượt tải: 0
20 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2758 | Lượt tải: 0 Hai mặt phẳng song song
Hai mặt phẳng song songVí dụ 1: Cho hai hình bình hành ABCD và ABEF không cùng thuộc một mặt phẳng và có chung cạnh AB. a) Chứng minh (AOF) // (BCE). b) Trên AC và BF lấy hai điểm M và N sao cho: AM/AC = BN/BF = 2/3 Qua N kẻ đường thẳng song song với AB cắt À tại (P). Chứng minh rằng (MNP)//(CDFE).
 39 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2344 | Lượt tải: 0
39 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2344 | Lượt tải: 0 Tích phân xác định
Tích phân xác địnhf(x) là hàm số liên tục trên [a, b], F(x) là một nguyên hàm của f(x) trên [a, b]. Hiệu số F(b) - F(a) được gọi là tích phân từ a đến b của f(x) và được ký hiệu là:
 19 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2422 | Lượt tải: 0
19 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2422 | Lượt tải: 0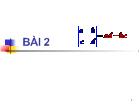 Đề tài Định thức (Slide)
Đề tài Định thức (Slide)Với mỗi ma trận vuông A cấp n tồn tại một số thực được gọi là định thức của ma trận A, được ký hiệu
 38 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2260 | Lượt tải: 0
38 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 2260 | Lượt tải: 0 Ma trận - Định thức (Slide)
Ma trận - Định thức (Slide)Định nghĩa ma trận: Một bảng số chữ nhật có m hàng và n cột gọi là ma trận cấp m x n aij là phần tử của ma trận A ở hàng i cột j. A = [aij]m x n = (aij)m x n Ma trận vuông: Khi m = n , gọi là ma trận vuông cấp n a11,a22,…ann được gọi là các phần tử chéo. Đường thẳng xuyên qua các phần tử chéo gọi là đường chéo chính.
 36 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 3397 | Lượt tải: 2
36 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 3397 | Lượt tải: 2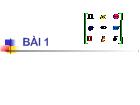 Chuyên đề Ma trận (slide)
Chuyên đề Ma trận (slide)Định nghĩa: Ma trận cỡ mxn là một bảng gồm m.n số thực (phức) được viết thành m hàng và n cột như sau: Kí hiệu: A = [aij]mxn Tập hợp tất cả các ma trận cỡ mxn được ký hiệu Mmxn * Khi m = n (số hàng = số cột) ta nói A là ma trận vuông cấp n. Tập hợp tất cả các ma trận vuông cấp n được ký hiệu Mn.
 31 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 3105 | Lượt tải: 0
31 trang | Chia sẻ: lylyngoc | Ngày: 15/03/2014 | Lượt xem: 3105 | Lượt tải: 0
Website đang trong thời gian thử nghiệm, chờ xin giấy phép của Bộ TT & TT.

