TimTaiLieu.vn - Tài liệu, ebook, giáo trình, đồ án, luận văn
Tổng hợp tất cả tài liệu, ebook, giáo trình Giải Tích - Đại Số chọn lọc và hay nhất.

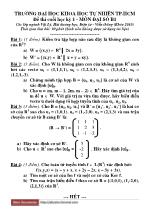 Đề thi cuối học kỳ môn Đại số B1 (Khóa 2010) - Đại học Khoa học Tự nhiên TP.HCM
Đề thi cuối học kỳ môn Đại số B1 (Khóa 2010) - Đại học Khoa học Tự nhiên TP.HCMBài 2: (3 điểm). Cho W là không gian con của không gian R* sinh bởi các vectơ u = (1,1,1,1), u = (1,2,3,3), u3 = (1,3,4,2), u4 = (1,2,1,-3). a) Chứng minh tập hợp B = {uh, uh, us} là cơ sở của W và xác định [u]B. b) Cho u = (m, m – 1, 2m, m - 2) + R'. Hãy tìm giá trị của | m để u 6 W. Với giá trị m vừa tìm được, hãy biểu diễn vectơ u dưới dạng t...
 3 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 477 | Lượt tải: 0
3 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 477 | Lượt tải: 0 Đề thi cuối học kỳ môn Đại số B1 (Khóa 2009) - Đại học Khoa học Tự nhiên TP.HCM
Đề thi cuối học kỳ môn Đại số B1 (Khóa 2009) - Đại học Khoa học Tự nhiên TP.HCMBài 1: (2,0 điểm). a) Cho ( ) Chứng minh rằng A khả nghịch khi và chỉ khi adj(A) khả nghịch (trong đó adj(A) là ma trận phó của A). b) Cho ( ) Chứng minh rằng AB khả nghịch khi và chỉ khi cà A và B cùng khả nghịch. Bài 2: (2,0 điểm). Trong R4 cho các vectơ ( ), ( ), ( ) và W là không gian con của R4 sinh bởi các vectơ . a) Chứng minh rằng tập hợp *...
 2 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 571 | Lượt tải: 0
2 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 571 | Lượt tải: 0 Bài giảng Phương pháp tham lam (Bản đẹp)
Bài giảng Phương pháp tham lam (Bản đẹp)+ Cho trước một tập A gồm n đối tượng, ta cần phải chọn một tập con S từ tập A. Với mỗi tập con S được chọn ra thỏa mãn các yêu cầu của bài toán, ta gọi là một nghiệm chấp nhận được. Nghiệm tối ưu là nghiệm chấp nhận được mà tại đó hàm mục tiêu đạt giá trị nhỏ nhất (lớn nhất). Ý tưởng tham lam: Xây dựng lời giải của bài toán với việc chấp nhận ...
 24 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 529 | Lượt tải: 0
24 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 529 | Lượt tải: 0 Phân tích dao động tự do vỏ trụ tròn bằng vật liệu rỗng theo lý thuyết biến dạng cắt bậc nhất
Phân tích dao động tự do vỏ trụ tròn bằng vật liệu rỗng theo lý thuyết biến dạng cắt bậc nhấtTÓM TẮT Bài báo sử dụng lý thuyết biến dạng cắt bậc nhất (FSDT) của Reissner-Mindlin để xây dựng lời giải tích phân tích dao động tự do của vỏ trụ tròn làm bằng vật liệu rỗng, tựa khớp trên hai cạnh biên. Mô đun đàn hồi và khối lượng riêng của vật liệu được giả thiết là hàm số của lỗ rỗng, biến đổi trơn và đối xứng theo phương chiều dày vỏ. Hệ ...
 10 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 615 | Lượt tải: 0
10 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 615 | Lượt tải: 0 Giới hạn banach và ứng dụng trong lý thuyết phương trình sai phân
Giới hạn banach và ứng dụng trong lý thuyết phương trình sai phânTóm tắt Tác giả sử dụng khái niệm giới hạn Banach để chứng minh một số khẳng định trong lý thuyết các phương trình sai phân tuyến tính, đưa ra một số ví dụ áp dụng các khẳng định này. Từ khóa: Giới hạn Banach, không gian Banach các dãy số thực bị chặn, phiếm hàm tuyến tính liên tục trên một không gian định chuẩn, Định lý Hahn-Banach, phương...
 6 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 522 | Lượt tải: 0
6 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 522 | Lượt tải: 0 Điều kiện tối ưu dạng xấp xỉ cho bài toán tối ưu đa trị
Điều kiện tối ưu dạng xấp xỉ cho bài toán tối ưu đa trịTÓM TẮT Từ các kết quả về điều kiện tối ưu cho bài toán tối ưu đa trị dựa trên khái niệm dưới vi phân yếu của hàm véc tơ, bài báo này trình bày nghiên cứu dưới vi phân xấp xỉ yếu cho hàm đa trị. Khái niệm -dưới vi phân yếu cho hàm đa trị được đề nghị. Điều kiện tối ưu xấp xỉ dạng Fritz-John và KuhnTucker cho bài toán được thiết lập. Từ khoá: tố...
 13 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 757 | Lượt tải: 0
13 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 757 | Lượt tải: 0 Đề xuất giải thuật di truyền giải bài toán xếp thời khóa biểu
Đề xuất giải thuật di truyền giải bài toán xếp thời khóa biểuTÓM TẮT Việc xếp thời khóa biểu hợp lý là bài toán tối ưu có nhiều ứng dụng trong thực tế. Được phân loại thuộc lớp NP-complete và đã được nghiên cứu rộng rãi trong hàng chục năm qua với các hướng tiếp cận như quy hoạch toán học, tối ưu dựa trên ràng buộc, tối ưu đa mục tiêu, giải thuật tham lam, giải thuật metaheuristic.v.v. Nghiên cứu này đề ...
 10 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 984 | Lượt tải: 0
10 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 984 | Lượt tải: 0 Bài giảng môn Toán cao cấp 1 - Chương 5c: Hồi qui và tương quan - Nguyễn Văn Tiến
Bài giảng môn Toán cao cấp 1 - Chương 5c: Hồi qui và tương quan - Nguyễn Văn TiếnPhân tích hồi quy • Phân tích hồi quy là tìm quan hệ phụ thuộc của một biến, được gọi là biến phụ thuộc vào một hoặc nhiều biến khác, được gọi là biến độc lập nhằm mục đích ước lượng hoặc tiên đoán giá trị kỳ vọng của biến phụ thuộc khi biết trước giá trị của biến độc lập. • Một số tên gọi khác của biến phụ thuộc và biến độc lập như sau: • ...
 21 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 518 | Lượt tải: 0
21 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 518 | Lượt tải: 0 Bài giảng môn Toán cao cấp 1 - Chương 5b: Quy hoạch tuyến tính hai biến - Nguyễn Văn Tiến
Bài giảng môn Toán cao cấp 1 - Chương 5b: Quy hoạch tuyến tính hai biến - Nguyễn Văn TiếnVí dụ 4 • Bài toán lập kế hoạch sản xuất • Một trại cưa các khúc gỗ thành các tấm ván. Có hai loại ván: ván thành phẩm và ván sử dụng trong xây dựng. Giả sử, đối với: • Ván thành phẩm cần 2 giờ để cưa và 5 giờ để bào 10m ván • Ván xây dựng cần 3 giờ để cưa và 3 giờ để bào 10m ván • Máy cưa làm việc tối đa 8 giờ trong ngày và máy bào làm vi...
 8 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 600 | Lượt tải: 0
8 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 600 | Lượt tải: 0 Bài giảng Toán cao cấp 1 - Chương 5a: Ma trận hệ phương trình tuyến tính - Nguyễn Văn Tiến
Bài giảng Toán cao cấp 1 - Chương 5a: Ma trận hệ phương trình tuyến tính - Nguyễn Văn TiếnMa trận bậc thang • Phần tử khác 0 đầu tiên của một hàng kể tử bên trái gọi là phần tử cơ sở của hàng đó. • Ma trận bậc thang: – Hàng không có phần tử cơ sở (nếu tồn tại) thì nằm dưới cùng. – Phần tử cơ sở của hàng dưới nằm về bên phải (không cùng cột) so với phần tử cơ sở của hàng trên.
 17 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 546 | Lượt tải: 0
17 trang | Chia sẻ: thanhle95 | Ngày: 15/07/2021 | Lượt xem: 546 | Lượt tải: 0
Website đang trong thời gian thử nghiệm, chờ xin giấy phép của Bộ TT & TT.

